Introduction to Hill Climbing | Artificial Intelligence

Hill climbing is a simple optimization algorithm used in Artificial Intelligence (AI) to find the best possible solution for a given problem. It belongs to the family of local search algorithms and is often used in optimization problems where the goal is to find the best solution from a set of possible solutions.

• In Hill Climbing, the algorithm starts with an initial solution and then iteratively makes small changes to it in order to improve the solution. These changes are based on a heuristic function that evaluates the quality of the solution. The algorithm continues to make these small changes until it reaches a local maximum, meaning that no further improvement can be made with the current set of moves.
• There are several variations of Hill Climbing, including steepest ascent Hill Climbing, first-choice Hill Climbing, and simulated annealing. In steepest ascent Hill Climbing, the algorithm evaluates all the possible moves from the current solution and selects the one that leads to the best improvement. In first-choice Hill Climbing, the algorithm randomly selects a move and accepts it if it leads to an improvement, regardless of whether it is the best move. Simulated annealing is a probabilistic variation of Hill Climbing that allows the algorithm to occasionally accept worse moves in order to avoid getting stuck in local maxima.

Hill Climbing can be useful in a variety of optimization problems, such as scheduling, route planning, and resource allocation. However, it has some limitations, such as the tendency to get stuck in local maxima and the lack of diversity in the search space. Therefore, it is often combined with other optimization techniques, such as genetic algorithms or simulated annealing, to overcome these limitations and improve the search results.

Advantages of Hill Climbing algorithm:

1. Hill Climbing is a simple and intuitive algorithm that is easy to understand and implement.
2. It can be used in a wide variety of optimization problems, including those with a large search space and complex constraints.
3. Hill Climbing is often very efficient in finding local optima, making it a good choice for problems where a good solution is needed quickly.
4. The algorithm can be easily modified and extended to include additional heuristics or constraints.

Disadvantages of Hill Climbing algorithm:

1. Hill Climbing can get stuck in local optima, meaning that it may not find the global optimum of the problem.
2. The algorithm is sensitive to the choice of initial solution, and a poor initial solution may result in a poor final solution.
3. Hill Climbing does not explore the search space very thoroughly, which can limit its ability to find better solutions.
4. It may be less effective than other optimization algorithms, such as genetic algorithms or simulated annealing, for certain types of problems.

Hill Climbing is a heuristic search used for mathematical optimization problems in the field of Artificial Intelligence.
Given a large set of inputs and a good heuristic function, it tries to find a sufficiently good solution to the problem. This solution may not be the global optimal maximum.

• In the above definition, mathematical optimization problems imply that hill-climbing solves the problems where we need to maximize or minimize a given real function by choosing values from the given inputs. Example-Travelling salesman problem where we need to minimize the distance traveled by the salesman.
• ‘Heuristic search’ means that this search algorithm may not find the optimal solution to the problem. However, it will give a good solution in a reasonable time.
• A heuristic function is a function that will rank all the possible alternatives at any branching step in the search algorithm based on the available information. It helps the algorithm to select the best route out of possible routes.

Features of Hill Climbing

1. Variant of generating and test algorithm:

It is a variant of generating and testing algorithms. The generate and test algorithm is as follows :

• Generate possible solutions.
• Test to see if this is the expected solution.
• If the solution has been found quit else go to step 1.

Hence we call Hill climbing a variant of generating and test algorithm as it takes the feedback from the test procedure. Then this feedback is utilized by the generator in deciding the next move in the search space.

2. Uses the Greedy approach:

At any point in state space, the search moves in that direction only which optimizes the cost of function with the hope of finding the optimal solution at the end.

Types of Hill Climbing

1. Simple Hill climbing:

It examines the neighboring nodes one by one and selects the first neighboring node which optimizes the current cost as the next node.

Algorithm for Simple Hill climbing :

• Evaluate the initial state. If it is a goal state then stop and return success. Otherwise, make the initial state as the current state.
• Loop until the solution state is found or there are no new operators present which can be applied to the current state.
  • Select a state that has not been yet applied to the current state and apply it to produce a new state.
  • Perform these to evaluate the new state.
    • If the current state is a goal state, then stop and return success.
    • If it is better than the current state, then make it the current state and proceed further.
    • If it is not better than the current state, then continue in the loop until a solution is found.

    2. Steepest-Ascent Hill climbing:

    It first examines all the neighboring nodes and then selects the node closest to the solution state as of the next node.

    Algorithm for Steepest Ascent Hill climbing :

    • Evaluate the initial state. If it is a goal state then stop and return success. Otherwise, make the initial state as the current state.
    • Repeat these steps until a solution is found or the current state does not change
      • Select a state that has not been yet applied to the current state.
      • Initialize a new ‘best state’ equal to the current state and apply it to produce a new state.
      • Perform these to evaluate the new state
        • If the current state is a goal state, then stop and return success.
        • If it is better than the best state, then make it the best state else continue the loop with another new state.

        3. Stochastic hill climbing:

        It does not examine all the neighboring nodes before deciding which node to select. It just selects a neighboring node at random and decides (based on the amount of improvement in that neighbor) whether to move to that neighbor or to examine another.

        • Evaluate the initial state. If it is a goal state then stop and return success. Otherwise, make the initial state the current state.
        • Repeat these steps until a solution is found or the current state does not change.
          • Select a state that has not been yet applied to the current state.
          • Apply the successor function to the current state and generate all the neighbor states.
          • Among the generated neighbor states which are better than the current state choose a state randomly (or based on some probability function).
          • If the chosen state is the goal state, then return success, else make it the current state and repeat step 2 of the second point.

          State Space diagram for Hill Climbing

          The state-space diagram is a graphical representation of the set of states our search algorithm can reach vs the value of our objective function(the function which we wish to maximize).

          • X-axis: denotes the state space ie states or configuration our algorithm may reach.
          • Y-axis: denotes the values of objective function corresponding to a particular state.

          The best solution will be a state space where the objective function has a maximum value(global maximum).

          

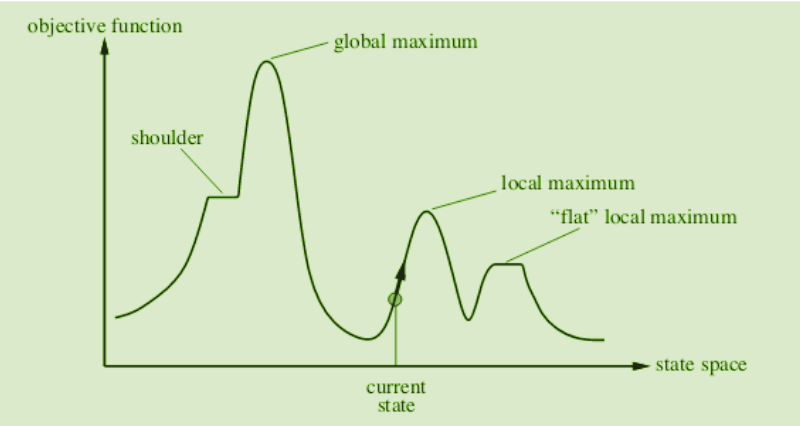
          Different regions in the State Space Diagram:

          • Local maximum: It is a state which is better than its neighboring state however there exists a state which is better than it(global maximum). This state is better because here the value of the objective function is higher than its neighbors.
            
          • Global maximum: It is the best possible state in the state space diagram. This is because, at this stage, the objective function has the highest value.
          • Plateau/flat local maximum: It is a flat region of state space where neighboring states have the same value.
          • Ridge: It is a region that is higher than its neighbors but itself has a slope. It is a special kind of local maximum.
          • Current state: The region of the state space diagram where we are currently present during the search.
          • Shoulder: It is a plateau that has an uphill edge.

          Problems in different regions in Hill climbing

          Hill climbing cannot reach the optimal/best state(global maximum) if it enters any of the following regions :

          • Local maximum: At a local maximum all neighboring states have a value that is worse than the current state. Since hill-climbing uses a greedy approach, it will not move to the worse state and terminate itself. The process will end even though a better solution may exist.
            To overcome the local maximum problem: Utilize the backtracking technique. Maintain a list of visited states. If the search reaches an undesirable state, it can backtrack to the previous configuration and explore a new path.
          • Plateau: On the plateau, all neighbors have the same value. Hence, it is not possible to select the best direction.
            To overcome plateaus: Make a big jump. Randomly select a state far away from the current state. Chances are that we will land in a non-plateau region.
          • Ridge: Any point on a ridge can look like a peak because movement in all possible directions is downward. Hence the algorithm stops when it reaches this state.
            To overcome Ridge: In this kind of obstacle, use two or more rules before testing. It implies moving in several directions at once.

          Here is a simple example of hill climbing in Python: